양창현 교수님의 수업을 직접 들었던 기억이 가물가물합니다. 고인이 되셨던 교수님의 수업을 들을 때는 정말 정말 공부가 싫었는데, 이렇게 다시 책을 펼쳐보니 새삼스럽고 더 열심히 해야 할 것 같은 생각을 하게 됩니다. 정역학의 단순보 반력을 시작으로 구조역학의 하나하나를 마이다스라는 해석 프로그램을 통해서 검증해 보고, 수작업으로 계산도 실제로 해보고 하나하나 내용을 만들어 볼까 합니다.
단순보의 반력 구하기 예제

보는 것처럼 단순보를 12개의 Element로 나누고, 절점(Node)는 13개로 만들어서 작성한 단순보의 모습입니다. 이곳에 6.000m에 2 tonf/m의 등분포하중이 작용을 하고, 경사진 30 tonf의 집중하중이 작용하는 모습을 볼 수 있습니다. 이러한 단순한 구조 system을 풀이하는 방법은 여러 가지가 있을 것 같습니다. 문제의 답이 반력이기 때문에 손으로 풀이를 하면 간단하지만, 이것을 유한요소해석 프로그램인 Midas Civil를 통해서 맞게 되는지를 검증하는 작업을 할 것입니다. 사실상 이러한 행동이 크게 의미는 없다고 보지만, 할 수 있고 없고의 차이가 점점 더 복잡하거나 예매한 구조물의 모델링을 하는데 도움이 될 수 있다는 것입니다.

마이다스 모델링 체크사항
마이다스 모델링에서 체크해야 할 사항은 X, Y, Z 축을 로컬좌표로 확인해야 하는 부분이 중요합니다. 이유는 로컬좌표를 이용해서 모멘트나 전단력의 값을 읽을 때 로컬좌표가 틀어져 있을 경우에는 다른 부재력의 양상을 보이기 때문에 항상 모델링에서 로컬좌표를 확인할 필요가 있습니다.
지점 조건의 경우에는 X축과 Z축에 대한 구속을 통해 잡으면 되는데, 로데이션이나 Y축의 경우 Structure-Type에서 X-Z Plane으로 해석을 하면 됩니다. 특이한 것은 경사진 하중을 재하 하는 것이 불가능하기 때문에 분력(X축 분력, Z 축 분력)으로 구분하여 하중을 재하해야 합니다.
또한 실제 문제와는 상관이 없지만, Material과 Section에 대한 정의가 되지 않는다면 해석이 불가능하기 때문에 가상으로 아무값이나 입력을 해주면 됩니다.

보는 것처럼 a점의 반력 Fz=15tonf, Fx=18 tonf, b점에는 Fz=21 tonf으로 정확히 결과값을 도출해 낼 수가 있습니다. 검산의 의미에서 프로그램을 이용해서 결과값을 확인할 수는 있지만, 이렇게 간단한 단순보의 반력계산의 경우는 계산문제로 많이 출제가 되는 부분이 있습니다.

그 이외에도 실제로 이러한 하중이 작용할 경우 발생할 수 있는 구조물의 변위를 조금 크게 육안으로 확인이 가능하도록 나타내주는 부분이 구현이 되는 것을 알 수 있습니다. 실제로 이러한 변위에 대한 값이 허용범위안에서 발생하게 되면 구조적으로 크게 문제가 되지는 않지만, 과도하게 발생할 경우에는 경계조건이나 잘못된 모델링이 만들어졌다는 것을 직감적으로 알 수 있는 척도가 될 수도 있으니 참고하면 좋을 것 같습니다. 항상 설계작업을 하거나 모델링을 통해서 상세해석등의 복잡한 업무를 수행할 경우 이러한 작은 변화와 결과값에 대한 이해와 논리적으로 앞뒤가 맞는지를 확인하는 습관은 매우 중요한 것이라고 개인적으로 생각합니다.
여기에서도 X-Dir으로 -6.619E-05라는 아주 미묘한 변위가 발생하는 것을 알 수 있습니다. 실제 0.06619mm로 1mm도 안되는 변화가 생기기는 하지만 어찌 되었든 b점의 경계조건이 X축으로 풀려 있기 때문에 움직이는 경향을 보이는 것이 당연한 결과일 것입니다. 만약에 묶여있다면 0이라는 값을 보일 것입니다.
Z-Dir으로 4.298mm의 처짐이 발생하는 것을 볼 수 있습니다. 실제로 이러한 형태의 구조물이 이러한 하중을 받을 일은 없지만 만약에 이렇게 하중을 받게 된다면 4mm의 처짐을 육감적으로 확인할 필요가 있습니다. 또한 ScaleFactor가 139.6이라는 숫자로 엄청나게 큰 값으로 보여주고 있다는 것을 확인할 수 있습니다.
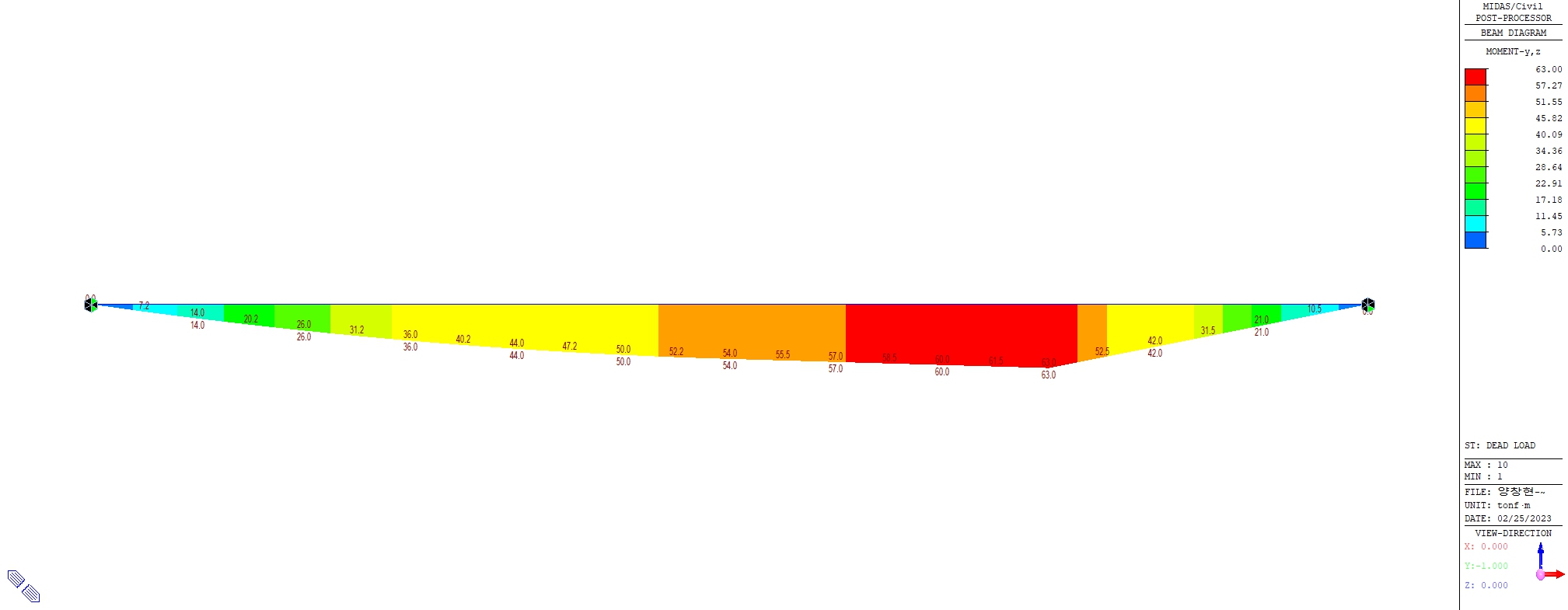
또한 하중에 의해 발생하는 모멘트의 Diagrams을 도출해 낼 수가 있습니다. 최대모멘트의 경우 63.0tonf·m가 발생한다는 것을 알 수 있습니다. 우리가 기본적으로 모멘트와 전단력을 찾아내는 이유는 구조물 설계법에서 사용하중과 계수하중, 극한한계상태하중, 사용한계상태하중 등 설계법에 따라 그 내용과 계수값을 달리하여 경우의 수를 이용해서 모멘트와 전단력을 뽑아내어 단면을 검토하는 것이기 때문에 모멘트 Diagram과 전단력 Diagram이 중요한 것입니다.
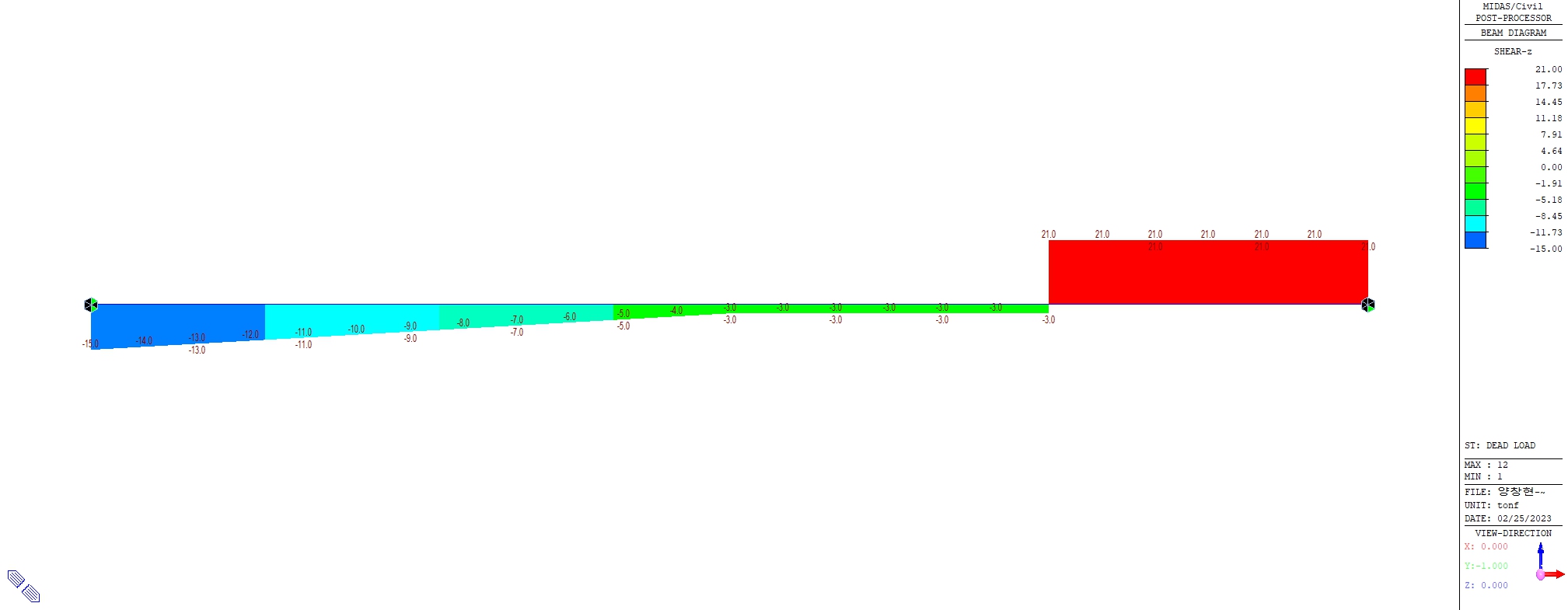
전단력도 역시 다양한 형태로 나타나면 나중에는 이러한 Diagram을 그리는 방법을 정정구조물이나 부정정구조물에서 쉽게 공부를 할 수가 있습니다. 어찌 되었든 이 구조물에서 어떤 형태로든 전단력이 발생하지만 빨간색의 21 tonf의 전단력이 발생하게 되며 이 값을 견디어 낼 수 있도록 단면을 설계하는 것이 중요합니다. 그 값을 견디어 내어야만 구조물의 안전성이 확보되기 때문입니다.
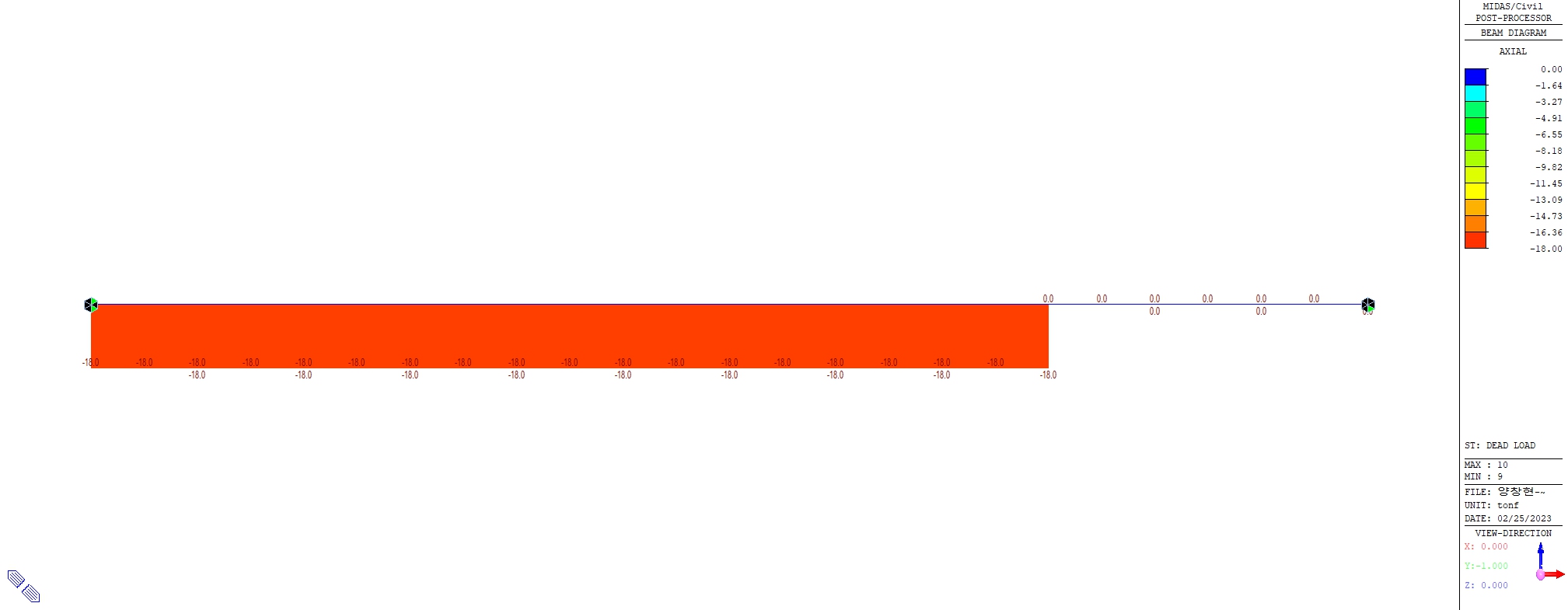
축력에 대한 Diagrams입니다. 압축력을 받는 것으로 값이 나타나며, 18tonf이라는 부재력이 발생하는 것을 확인할 수 있습니다.
마이다스를 사용하고 나서
이처럼 마이다스라는 구조해석 프로그램을 이용해서 실제 구조물을 이상화한 상태에서 각 부재의 위치별 부재력을 읽고 흐름을 파악할 수 있다는 것이 중요합니다. 실제로 이러한 부분들이 대학을 다닐 때는 그냥 문제로만 시험을 보아야 하니 받아들이곤 했지만, 어느 정도 식견이 쌓이고 바라보는 것이 다르지는 않지만 생각하는 접근방식에서 차이를 보이는 것 같습니다. 실제로 하천에 위치한 단경간 교량에 이러한 하중을 재하하고 구조적인 해석이 필요하다면 분명 마이다스를 이용해서 모델링하고 해석을 실시하고, 구조적인 해석과 단면검토를 통해 구조적인 안전성을 판단하든지 설계를 하는 일을 진행할 수 있을 것이라고 판단할 것 같습니다.
'토목교육자료' 카테고리의 다른 글
| [교육자료] 교량구조물_콘크리트교량 (1) | 2023.10.04 |
|---|---|
| [교육자료] 교량의 인식 (4) | 2023.10.03 |
| 마이다스로 검증해 본 구조역학_내민보의 반력 구하기 (1) | 2023.03.24 |
| AutoCad 기본명령어 정리하기 (2) | 2023.03.04 |
| [교육자료] 교량의 인식 (0) | 2022.10.31 |



